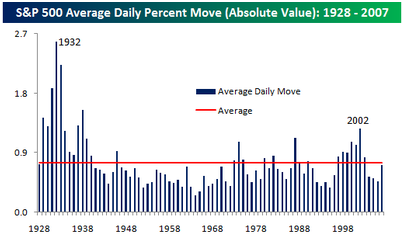
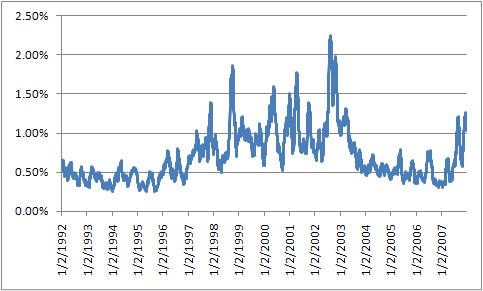
Tue 27 Sep 2011
Eddy Elfenbein recently put forward a simple model relating gold prices and interest rates:
The key insight is that Gibson’s Paradox never went away. It still exists, just in a different form. I got this idea from a 1988 paper by Larry Summers and Robert Barsky, “Gibson’s Paradox and the Gold Standard.”
Where I differ from Summers and Barsky is that I focused on short-term interest rates while they focused on long-term rates. Well, with Operation Twist we got a perfect test of who’s right.
The Fed’s new plan is to sell short-term Treasury bills and buy long-term Treasury bonds. This means that long-rates will be pushed down and short-rates will be pushed up. If gold rises, then Barsky and Summers are right; if gold falls, then I’m right.
At this point Elfenbein is only talking about correlations. But as he continues to discusses his model, he seems to take a causal stance:
I said in my original post that the price of gold is basically a political decision. The Fed can change the game anytime they want to. I can’t say whether this will lead to a long-term decline in gold. That will depend on inflation and interest rates. But for now, the gold market is clearly observing the short end of the yield curve.
I don’t want to presume too much about Elfenbein’s belief about any potential causation. But it’s still an interesting question: is there any evidence of causation? If so, in which direction does it run? (more…)